Understanding Stability in LNA Design

When it comes to designing Low-Noise Amplifiers (LNAs), ensuring stability is paramount. Stability refers to the amplifier’s ability to avoid oscillations, which can be detrimental to performance. Understanding stability types and the conditions under which an LNA remains stable is crucial for successful design.

Stability Types:

Unconditional Stability: Unconditional stability implies that the LNA remains stable under all passive source and load impedances. Mathematically, it’s achieved when both the input reflection coefficient (|Γin|) and the output reflection coefficient (|Γout|) are less than 1.

Conditional Stability: Conditional stability, on the other hand, means that the LNA is stable only within a certain range of passive source and load impedances. This scenario, sometimes termed as potentially unstable, demands careful consideration as stability may vary based on the impedance conditions.

Satisfying Stability Conditions:

To ensure stability in amplifier design, we must meet the following conditions:

• |Γin| < 1
• |Γout| < 1

These conditions are fundamental for preventing oscillations and maintaining the amplifier’s performance within acceptable bounds.

Deriving the Stability Circle Equation:

Starting with the scattering (S) parameters:

S11​ = Reflection coefficient at the input
S12​ = Forward transmission parameter from port 2 to port 1
S21​ = Forward transmission parameter from port 1 to port 2
S22​ = Reflection coefficient at the output

The stability condition for an LNA can be represented in terms of the input and output reflection coefficients (Γin​ and Γout​): ∣S11​+S12​ΓL​S21​Γin​∣=1

Where:

• ΓL​ is the load reflection coefficient.
• Γin​ is the input reflection coefficient.

Now, let’s substitute Γin​=S11​+S12​ΓL​ (using the definition of input reflection coefficient) into the stability condition equation:

This equation represents the condition for stability in terms of the scattering parameters and the load reflection coefficient. It’s a valuable tool for analyzing stability in LNA design.

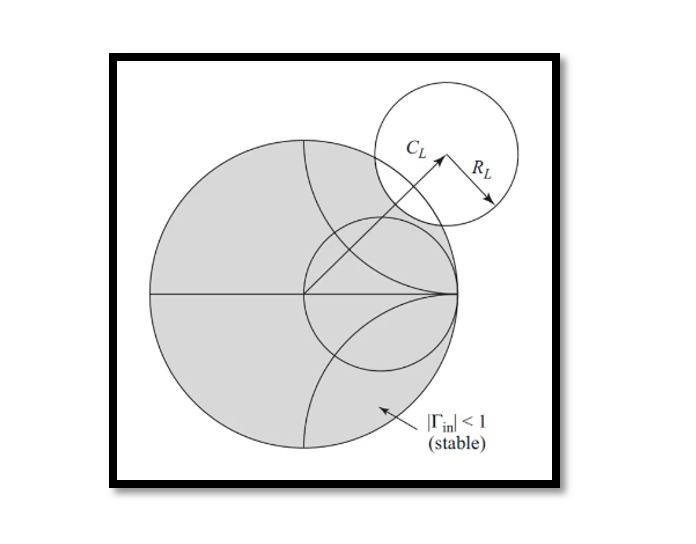
1. Find Center and Radii for Source and Load Side:
   • The stability circles on the Smith chart represent the locus of points where the amplifier remains stable. To begin, determine the center and radii of the stability circles corresponding to both the source and load sides.
2. Check to See Which Region is Stable:
   • Once the stability circles are plotted, identify the region(s) on the Smith chart where both the input and output stability conditions are satisfied. These regions represent stable operating conditions for the amplifier.
3. Try with an Arbitrary Load like ZL​=Z0​:
   • One common approach is to initially assume a normalized load impedance (ZL​=Z0​), where Z0​ is the characteristic impedance of the transmission line. This simplifies calculations and serves as a starting point for stability analysis.
4. Determine ΓL​ for this Load:
   • Calculate the reflection coefficient (ΓL​) for the assumed load impedance (ZL​=Z0​). This value will be used to evaluate stability conditions.
5. If ΓL​=0:
   • When the load reflection coefficient (ΓL​) is zero, it simplifies the stability condition equation to ∣Γin​∣=∣S11​∣=1. This means that the stability condition reduces to the magnitude of S11​ being equal to 1.
6. Check if |S11​∣<1 or ∣S11​∣>1:
   • Evaluate the magnitude of S11​. If ∣S11​∣<1, the amplifier is unconditionally stable for the given load impedance. Conversely, if ∣S11​∣>1, it indicates potential instability.
7. Check on Smith Chart:
   • Utilize the Smith chart to visually verify the stability of the amplifier. Plot S11​ on the chart and ensure it falls within the stable region(s) identified earlier. Adjust load impedance if necessary, to achieve stability.

By following these steps and utilizing tools like the Smith chart, designers can effectively evaluate and ensure the stability of LNAs, critical for reliable performance in various applications.

Conclusion:

In LNA design, stability is not merely a desirable trait but a critical requirement. Unstable amplifiers can lead to oscillations, distortion, and ultimately compromise system performance. By grasping the concepts of unconditional and conditional stability, and utilizing tools like the stability circle equation, designers can create LNAs that deliver reliable and robust performance across diverse operating conditions.