What is Dynamic Range and SFDR in Radio Frequency?
What is Dynamic Range?
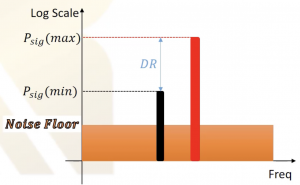
Dynamic range is the maximum input level that a receiver can tolerate divided by the minimum input level signal, which is defined as sensitivity. Dynamic range is equal to a maximum power of signal over minimum power signal at the system’s input. Converting this to log domain, we get the difference between maximum acceptable power Psig, in(max) in dBm, and minimum acceptable power Psig(min).
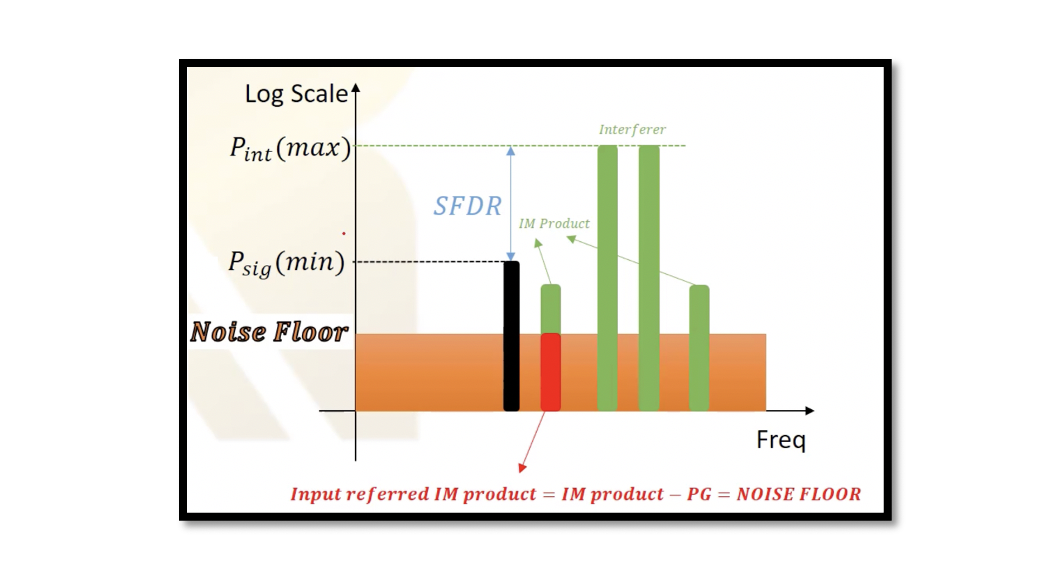
As stated in the previous section, sensitivity in radio frequency, the minimum acceptable power, is defined by the Psensitivity. Therefore, as shown in the figure below, we cannot decrease the input signal power level less than the Psig(min) value; otherwise, the signal won’t be detected. Similarly, there is an upper limit where we cannot increase the signal power more than this value.
A similar condition was seen in the section non-linearity, where it was stated that we are not allowed to increase our amplitude more than a specific value; otherwise, the system will experience gain compression, and this value is A-1dB or A1dB.
Similarly, we can say that Psig(max), the maximum level of the signal power, is equal to the power of 1dB. If the input power increases more than this value, then the system will experience compression, and it will become non-linear and will not work properly. So dynamic range in the log domain is defined as the difference between the maximum signal power and minimum signal power.
Spurious Free Dynamic Range (SFDR)?
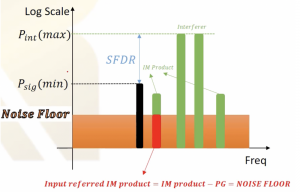
Now we are analysing the dynamic range with interferer existing in the system. The relationship between interferer noise is included in the definition of SFDR. As shown in the above figure, the lower limit, the minimum signal power is the Psensitivity. The upper limit here is the maximum power of the interferer but under some conditions. SFDR is the difference between these two maximum and minimum values. The maximum power of interferer Pint(max) can be defined as the maximum power limit for the system when input referred 3rd order intermodulation (IM) product does not exceed noise floor.
What is an input-referred IM product?
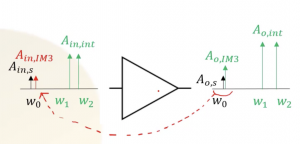
We have interferers at the input, and because of the non-linearity, the 3rd order IM product will appear in our channel, and it will block the signal.
The output IM3 or third-order IM product (Ao, IM3) at the output can be referred to as the input of the amplifier block (it can be any block, system, or a whole system), so Ain, IM3 is called the input preferred IM product. We have to be careful to note that this is just a comparison as Ain, IM3 doesn’t have a physical existence, we don’t really have such a signal. However, Ao, IM3 is real at the output, which acts as a blocker, but we don’t have Ain, IM3. So to define SFDR we have to make this kind of definition here by referring output IM3 to the input.
If we subtract power gain in the log domain from the output power of the IM product, we can find the input power of the input-referred IM product.
SFDR: If we increase the power more than the value Pint(max), the power of the input-referred IM product will increase more than the noise floor, which we don’t want. We want the power to be less or equal to the noise floor. So, this defines the upper limit of SFDR. Therefore, the relationship between the maximum and minimum power in terms of power gain would be: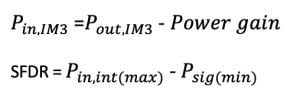
Finding SFDR for a system
We can find IIP3 in terms of input amplitude and output amplitude of interferers and IM product at the output, and the equation would be:
Using the above equation, we can find the interferer input power in terms of IIP3 power and input-referred IM3 power. When Pin, int is max, the input-referred IM3 power should not exceed the noise floor.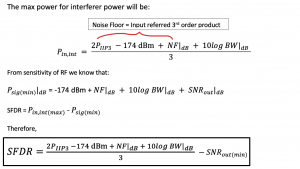
Example Question for SFDR:
Find the SFDR for a GSM receiver with SNRout(min) = 12 dB, Channel bandwidth of 200KHz, PIIP3 = 15, and Noise Figure of 9 dB.
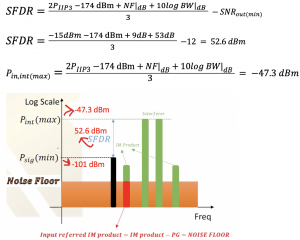
Therefore, SFDR is 52.6 dBm, and the signal power cannot be less than -101 dBm, and interferer power shouldn’t be higher than 47.3 dBm.
Learn more about this topic by taking the complete course ‘’RF Design Theory and Principles – RAHRF201’’.
Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/
Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.
