High and Low Injection – Implementing 90˚ Phase shift

Quadrature Down Conversion – High Injection

Previously we discussed about methods for implementing a 90˚ phase shift. Read about the methods to implement a 90-degree phase shift in a receiver. The first method is the RC-CR network, and the second method is Quadrature down conversion.  In this blog, we will show high and low injection, let’s start with an RF signal as shown in figure 1 below. It is in phase and is multiplied by a cosine wave (Fourier transform) to have a phase shift which gives us w_IF = w_LO-w_c (w_LO>w_c).

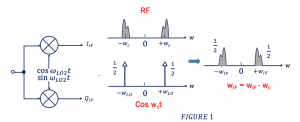
Figure 2 shows the convolution using a sine wave. Let’s say we have a channel (Ch) so, ch(w-w_c)+ch(w+wc), as shown in the figure, assume this channel is modulated and around w_c. So we will do a down conversion to bring it back to IF. We are convolving with a sine wave, see the equations below:

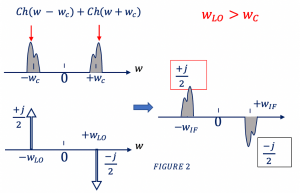
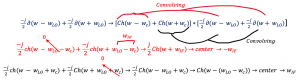
As we have a low pass filter, we can remove the high-frequency components in the equation, and it becomes 0. From the equation, we can see that the center frequency is -w_IF. Similarly, for the second part of convolution, we can see that the center frequency equals w_IF. The output in the figure shows the same thing, for a center frequency of w_IF we have -j/2 and for the center frequency of -w_IF we have +j/2.

Quadrature Down Conversion – Low injection

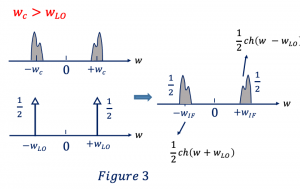
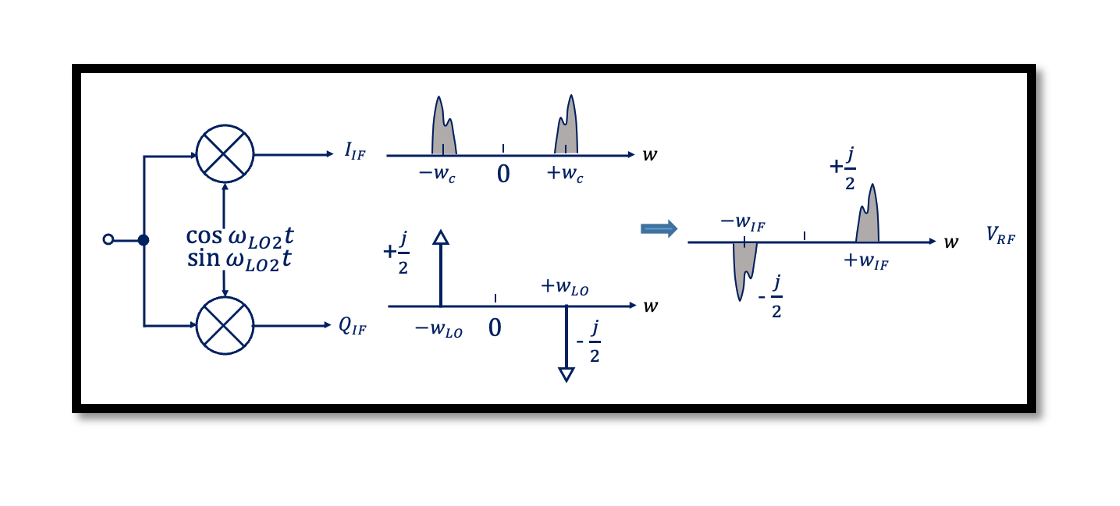
With a similar method now we will find low injection. For cosine part it is shown in Figure 3. For the sine wave, again we will do convolution, equations are as shown below. High-frequency components get cancelled. For low injection w_c > w_LO. The output we get is the center frequency of w_IF we have j/2 and for -w_IF we have -j/2. It is opposite to what we found in high injection.

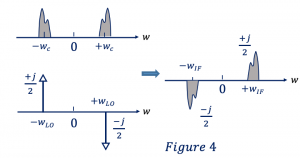
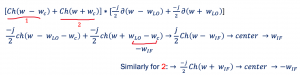
To remember easily:

For high side injection, the positive frequency part will turn clockwise (ClK) 90 degrees and for a high injection, the negative parts will turn anticlockwise (AClK).

For the low side its exactly the opposite. Use these formulas in order to find the quadrature part but for the in-phase part you don’t have to use any formula, in phase part is always positive because we are doing the frequency shift and we convolve the real part, so it doesn’t need a formula.

Learn more about this topic by taking the complete course ‘RF System Design of Receivers, Transmitters & Transceivers – RAHRF409’. Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/. Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.