Introduction to Harmonics in RF Systems

Harmonics play a crucial role in understanding the behavior of non-linear systems, particularly in the realm of RF (Radio Frequency). For those navigating careers in RF, the need to measure harmonics is inevitable. In this exploration, we’ll delve into the fundamentals of harmonics and examine the methods for their measurement. Typically expressed in dBm, the power of harmonics can vary in representation but is fundamentally rooted in the non-linear effects within a system. These effects are often attributed to non-linear loads or instances where the voltage-to-current output deviates from linearity. In linear systems, the presence of harmonics is negligible. So, what exactly do harmonics look like? They mirror the fundamental frequency and manifest as multiples of it. For instance, if the fundamental frequency is set at one gigahertz, the first harmonic will occur at 2GHz, followed by subsequent harmonics at 3GHz, 4GHz, 5GHz, and so forth. Additionally, the power of a harmonic diminishes in amplitude as its frequency increases. Harmonics can also be evaluated in terms of relative power, expressed in dBc, which denotes the power difference between the fundamental tone and its corresponding harmonic. Various components contribute to the generation of harmonics, including transistors, power amplifiers, switches, voltage-controlled oscillators (VCOs), mixers, switching mode power supplies, and certain magnetic passive devices. Understanding these elements is essential for effective harmonic analysis in RF systems.

Measurement Techniques for Harmonics in RF Systems

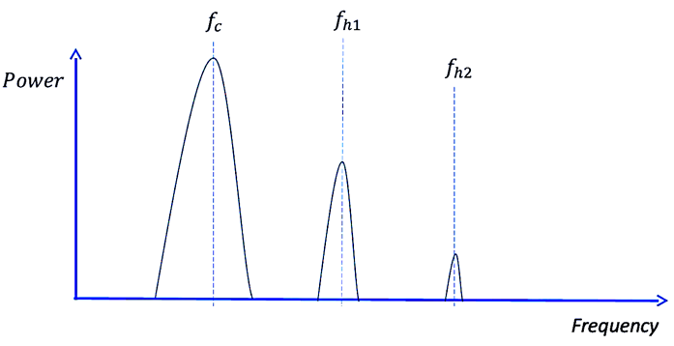
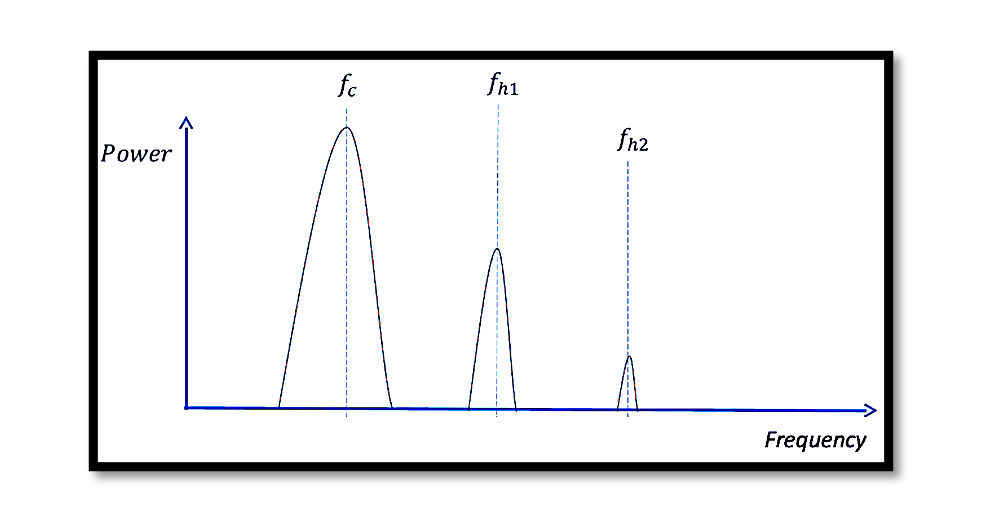
Now that we have a grasp of what harmonics entail, let’s explore the methods employed to measure them. In the accompanying image and power versus frequency graph, we observe the fundamental tone denoted by fc, exhibiting a notably higher power level compared to its harmonics. As mentioned earlier, the power levels of harmonics decrease with increasing frequency. The first harmonic (fh1) is illustrated with a lower power level, and its frequency is twice that of the fundamental frequency. The second harmonic (fh2) occurs at three times the fundamental frequency, with a further drop in power.

To measure harmonics, a setup like the one depicted here can be utilized. It’s crucial to note that a power sensor, as shown, lacks the capability to distinguish between frequencies in a wide spectrum. It provides the total power reading without specifying the output power for each individual tone. Suppose your RF source is the input to a power amplifier, a common harmonic generator. In this scenario, an attenuator precedes the power amplifier, serving two purposes: to attenuate the signal if it’s too strong and to present a favourable reflection coefficient to the power amplifier. The signal then splits into two paths using a power splitter. The first path incorporates attenuators and a switch, while the second path includes a high-pass filter and another part of the switch. The switch alternates between these paths, allowing only one to be read by the power sensor at a time.

A drawback of power sensors is their high noise floor, prompting consideration for alternatives such as a spectrum analyzer. The spectrum analyzer offers a lower noise floor and improved harmonic measurement capabilities. In either case, when utilizing both paths, the first path, passing through attenuators, is dedicated to measuring the fundamental frequency. This not only measures the fundamental power but also attenuates the harmonics to a level where they are no longer significant to the overall power. The inclusion of attenuators in this path ensures that tones such as fh1 and fh2 may become imperceptible, leaving only the fundamental frequency fc.

Enhancing Reflection Coefficient in Harmonic Measurement Setup

Continuing our exploration of harmonic measurement setups, let’s delve into the strategic placement of an attenuator after the power amplifier (PA) for an improved reflection coefficient. The power amplifier is typically matched to a characteristic impedance, often 50 ohms. However, many filters, including high pass filters commonly used, are reflective in nature. In other words, they reflect power at their input frequencies instead of fully blocking them. When the fundamental frequency reaches the high pass filter, it undergoes reflection.

Here’s where the attenuator post-PA becomes crucial. If, for instance, the signal was attenuated by 10dB in the initial passage through the attenuator, even when it gets reflected and returns, it has already lost a significant amount of power. Now, upon encountering the reflective filter, despite the possibility of some power being reflected back, the attenuator acts once more to attenuate the signal. In total, there’s a cumulative attenuation of 20dB. This strategic use of the attenuator creates an illusion for the power amplifier, making it appear as if it exhibits a highly favourable reflection coefficient, and mitigating the impact of reflected waves from the load. This nuanced approach aids in achieving more accurate and reliable harmonic measurements in RF systems.

Optimal Harmonic Measurement Setup for Sensitive DUTs

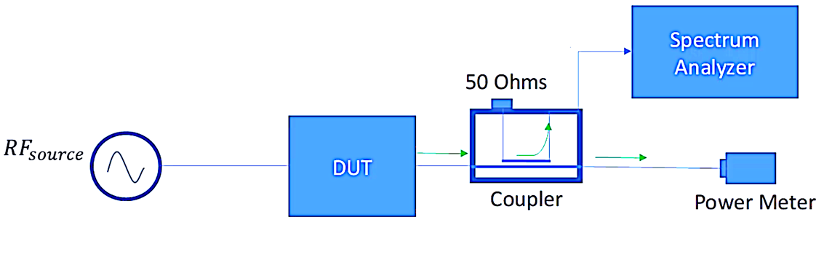
Illustrating a different approach to harmonic measurement, consider a setup comprising an RF source, Device Under Test (DUT), a coupler, a power meter, and a spectrum analyzer. Certain DUTs, such as power amplifiers, are highly sensitive to the load they encounter. In contrast to the previous example with a reflective filter, the coupler and power meter in this scenario are both configured to match the 50-ohm characteristic impedance. This ensures that the DUT perceives a 50-ohm load at its output.

This adjustment is critical as some reflected power from components like filters in the previous example could lead to an altered load impedance, potentially causing inaccuracies in power measurements. By maintaining a consistent 50-ohm impedance throughout the setup, potential issues with load sensitivity are mitigated. In this setup, the coupler allows a portion of the power to be coupled through its coupling port and fed into a spectrum analyzer. This configuration enables precise measurement of harmonics, offering a more accurate representation of the DUT’s performance. Notably, this approach minimizes reflections in the direct path, ensuring that the power amplifier’s measurements reflect its true power characteristics.

For additional control and customization, a high-pass filter can be introduced into the coupled path, providing further refinement of the harmonic measurement. Moreover, if necessary, an attenuator can be strategically placed between the DUT and the coupler to optimize the power levels and enhance the overall reliability of the harmonic measurements. This adaptable setup serves as a versatile solution, particularly beneficial when dealing with sensitive DUTs that demand precise and artifact-free measurements.

Conclusion:

In conclusion, understanding and accurately measuring harmonics are imperative for professionals navigating the intricate landscape of RF systems. Harmonics, often originating from non-linear effects in systems, present challenges and opportunities for precise assessment. Whether employing setups with reflective filters and strategic attenuators or configuring impedance-matched setups with couplers and spectrum analyzers, the nuances of harmonic measurements require careful consideration. The strategic placement of components, such as attenuators and high-pass filters, plays a pivotal role in optimizing measurement accuracy, especially when dealing with sensitive Devices Under Test (DUTs). As we navigate the complexities of harmonic measurement setups, it becomes evident that a tailored approach, considering the characteristics of the DUT and the desired measurement outcomes, is essential. By embracing versatile configurations and leveraging advanced tools like spectrum analyzers, professionals can ensure reliable and insightful harmonic measurements, contributing to the robustness and efficiency of RF systems.

Learn more about this topic by taking the complete course ‘Introduction to RF Testing Fundamentals and RF Test Architecture – RAHRF412’. Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/. Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.