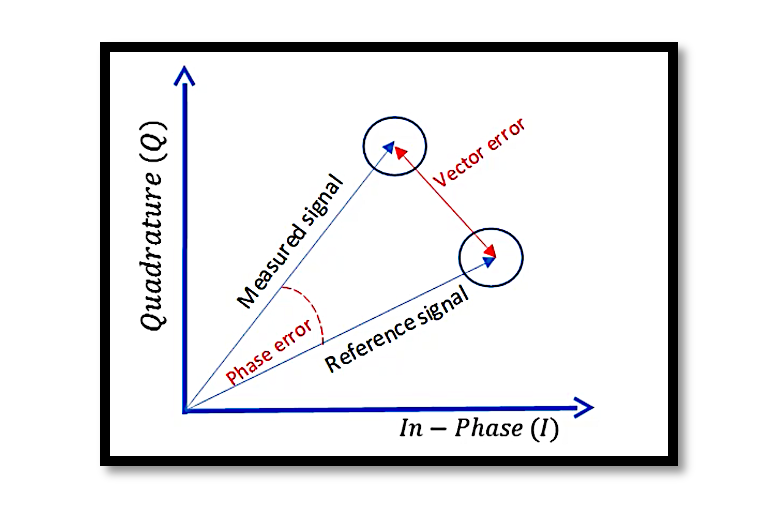
Error Vector Magnitude (EVM) in Signal Analysis

Error Vector Magnitude (EVM) is a critical parameter in the realm of signal analysis, particularly within the domain of wireless communication systems. This metric provides a quantitative measure of the difference between an ideal, or reference, modulated signal and the signal that is actually transmitted. By assessing the accuracy of the modulation process, EVM offers valuable insights into the quality and reliability of a communication system.

The Role of EVM Testing:

To conduct EVM testing effectively, a Vector Signal Analyzer (VSA) is commonly employed. The VSA plays a pivotal role in scrutinizing the modulated signal, providing detailed measurements of both its phase and amplitude. This dual measurement capability allows engineers and technicians to gain a comprehensive understanding of the signal’s characteristics, enabling them to identify and address potential issues impacting the overall quality of the transmission.

Key Components of EVM Measurement:

A fundamental requirement for precise EVM measurements is a thorough knowledge of the waveform used by either the Vector Signal Generator (VSG) or the Device Under Test (DUT). The VSA relies on this information to establish a baseline for comparison, highlighting any discrepancies in the signal’s phase and amplitude. This process is crucial for isolating and rectifying distortions or imperfections in the modulation process, contributing to the optimization of the communication system’s performance.

Dynamic EVM Assessments:

In addition to static EVM measurements, dynamic assessments that consider variations in input or output power levels are often conducted. Analyzing EVM against changing power conditions provides valuable insights into the transmitter chain’s behavior under different operating scenarios. Engineers can use this information to fine-tune the system, ensuring robust performance even in dynamic and challenging environments.

Modulation Density and EVM Limits:

It’s important to recognize that EVM does not have a universal limit; rather, its acceptable values depend on the density of the modulation being employed. Different modulation schemes have distinct tolerances for EVM, necessitating a tailored approach to assessment. Engineers must consider the specific modulation scheme in use to establish appropriate benchmarks and ensure that the system meets the required quality standards.

Defining Error Vector Magnitude

Error Vector Magnitude, commonly known as EVM, plays a crucial role in assessing the fidelity of a transmitted modulated signal by comparing it to an ideal reference value. This metric serves as a reliable indicator of the overall modulation quality within a transmitter chain.

In the realm of wireless communication, evaluating the EVM of a transmitted signal is a typical and fundamental measurement. The objective is to gauge the effectiveness of the transmitter chain and ensure that the modulation process is achieving the desired quality standards.

One of the primary culprits behind a poor EVM reading is often traced back to up-conversion (mixing) issues and insufficient linearity in RF power amplifiers. These challenges can introduce distortions in the signal, compromising its accuracy and reliability. As a result, understanding and addressing these factors are crucial for optimizing the performance of a communication system.

It’s important to note that EVM is not a one-size-fits-all metric, as its acceptable limits vary based on the density of the modulation being employed. The modulation density directly influences the maximum allowable EVM, making it imperative to tailor expectations and assessments according to the specific modulation scheme in use. By doing so, engineers and technicians can effectively pinpoint and rectify issues that might arise, ensuring a robust and high-quality transmission.

Error Vector Magnitude Measurement

• EVM testing needs a vector signal analyser (VSA)
• A VSA measures phase and amplitude
• The waveform used by the VSG or DUT must be known by the VSA
• EVM versus input/output power is sometimes measured.

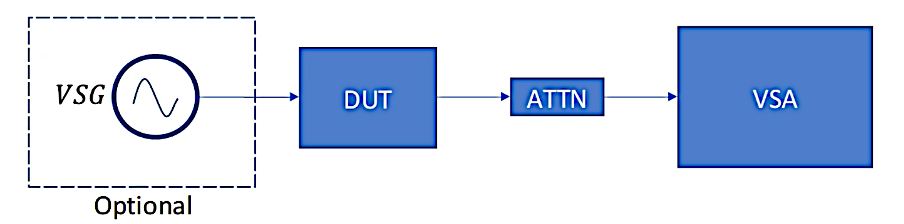
To conduct Error Vector Magnitude (EVM) measurements effectively, employing a Vector Signal Analyzer (VSA) is indispensable. The VSA serves as a critical tool in this process, allowing for the comprehensive analysis of the modulated signal by measuring both its phase and amplitude characteristics.

A crucial prerequisite for accurate EVM testing is a thorough understanding of the waveform used by either the Vector Signal Generator (VSG) or the Device Under Test (DUT). This knowledge is vital for the VSA to establish a baseline and accurately compare the transmitted signal against the ideal reference values. The VSA relies on this understanding to quantify any discrepancies in the phase and amplitude of the signal, providing valuable insights into the modulation quality.

In certain scenarios, EVM measurements are extended to assess the performance across varying input or output power levels. This involves analyzing how the EVM metric changes in relation to fluctuations in power. Such assessments contribute to a more comprehensive understanding of the transmitter chain’s behavior under different operating conditions, allowing for targeted adjustments and optimizations.

In summary, the EVM measurement process necessitates the utilization of a VSA, a tool proficient in evaluating both phase and amplitude characteristics. Additionally, a clear knowledge of the waveform utilized in the transmission is essential for accurate comparisons. The incorporation of power level assessments further enhances the diagnostic capabilities, offering a nuanced perspective on the modulation quality in dynamic operational scenarios.

Learn more about this topic by taking the complete course ‘Introduction to RF Testing Fundamentals and RF Test Architecture – RAHRF412’. Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/. Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.