Understanding Power Gain in Two-Port Networks

In two-port networks, the concept of power gain holds significant importance, offering multiple definitions crucial for the design and analysis of amplifiers. These definitions are interrelated, providing a comprehensive framework to optimize amplifier performance.

As we delve deeper, we’ll craft various expressions to quantify the gain, specifically targeting power amplification. It’s essential to emphasize that when we refer to gain, we inherently imply power amplification, signifying the augmentation of signal power within the system. Thus, our journey involves the development of expressions tailored to gauge the gain of two-port amplifiers.

These expressions are intricately woven with scattering parameters (S-parameters) of the transistor, necessitating a thorough understanding of these parameters. Extracted from the transistor, these S-parameters serve as foundational elements for computing power gains. Whether you’re working with an integrated circuit (IC) or a discrete transistor in a microwave circuit design, the availability of S-parameters empowers you to decipher the amplification potential of the system.

Consider a scenario where you’re tasked with designing a microwave circuit on a board. Armed with the S-parameters of the transistor, obtained either through procurement or extraction, you embark on the journey of exploring power gains. These gains not only quantify the amplification achieved but also offer insights into optimization strategies, including impedance matching, crucial for enhancing amplifier performance.

In essence, our pursuit of understanding power gains and their associated equations stems from the fundamental goal of amplification: to elevate input power, amplify it significantly, and deliver this amplified power efficiently. By laying the groundwork with power gains, we pave the way for comprehensive amplifier design and optimization.

In our exploration of two-port networks, we encounter three distinct types of power gains, each offering unique insights into amplifier performance:

• Power Gain
• Available Power Gain
• Transducer Power Gain

Now, let’s delve into each of these definitions, unraveling their intricacies and understanding their practical implications.

Let’s embark on a detailed examination of these three power gains, beginning with the foundational concept of power gain. Within this context, we’ll elucidate how power gain is defined and its relevance in amplifier analysis and design.

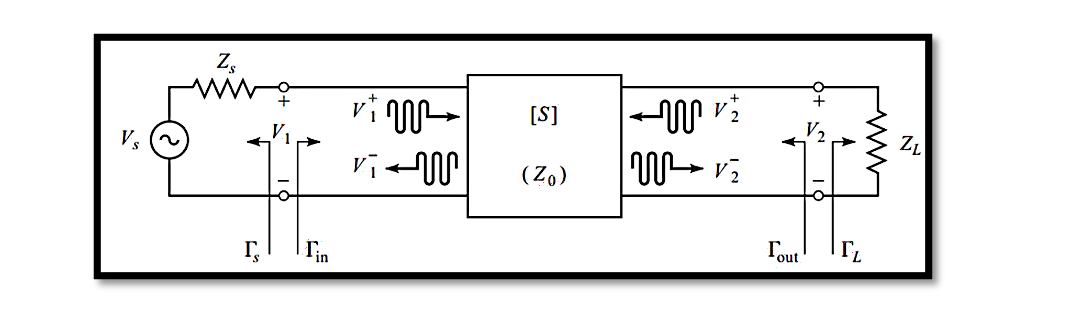
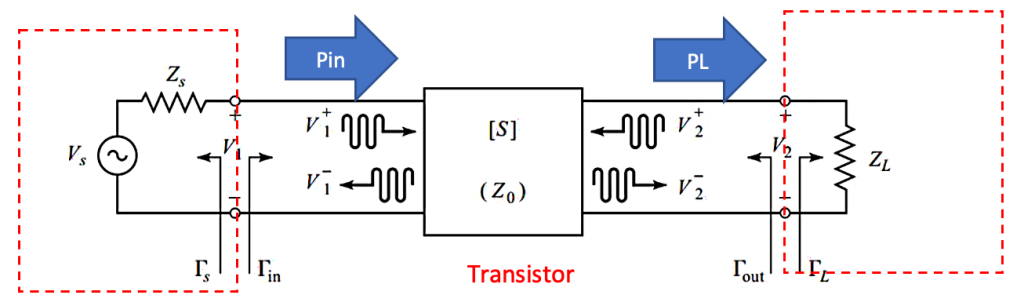
Consider the schematic depicted below, illustrating a transistor integrated within the circuit alongside load impedance (ZL) and source impedance (Zs). As we’ve elucidated in prior discussions, the left side of the circuit represents the output impedance of the input matching, while the right side denotes the input impedance of output matching. This schematic serves as the canvas upon which we’ll paint a clearer picture of power gain and its practical implications.

In our analysis of power gain within two-port networks, we find ourselves amidst the intricate structure of matching circuits enveloping a transistor. This configuration forms the foundation upon which we discern the essence of power gain.

Within this setup, the definition of power gain, denoted as PL/Pin, assumes paramount importance. Let’s delve into the components of this ex pression. Firstly, PL represents the power delivered to the load, denoted by ZL, where ZL manifests as a combination of real (RL) and imaginary (XL) components. As we’ve reiterated previously, the average power delivered to the load equates to half the real part of the voltage phasor (V2) multiplied by the conjugate of the current (I2) flowing through the load. This average power, designated as PL, serves as a crucial metric in evaluating the efficacy of power transfer to the load.

Power Delivered to the Transistor or Two-Port Network (Pin): Pin encompasses the total power delivered to the transistor or two-port network, accounting for all power inputs into the system. This includes the power supplied at the source as well as any losses or dissipations within the network.

Power Gain (PL/Pin): The power gain ratio, denoted as PL/Pin, quantifies the relationship between the power delivered to the load (PL) and the power delivered to the input of the two-port network (Pin). This ratio serves as a pivotal metric in evaluating the efficiency and effectiveness of power transfer within the system.

Now, turning our attention to Pin, we encounter the power delivered to the transistor or the two-port network. It’s imperative to discern that Pin isn’t merely the power supplied at the source; rather, it encompasses the power delivered to the entire two-port network. This distinction is vital in accurately assessing the power dynamics within the system.

In essence, the power gain ratio elucidates the relationship between the power dissipated or delivered to the load (PL) and the power delivered to the input of the two-port network (Pin). This delineation underscores the significance of comprehending Pin as the pivotal metric encompassing the entirety of power input to the network.

Exploring the Independence of Power Gain from Source Impedance (Zs)

The question arises: Is the power gain independent of Zs, the source impedance? Indeed, the power gain remains unaffected by changes in Zs. Let’s dissect this assertion to understand its implications.

When considering the power gain at the input of the network, the focus lies on the power delivered to the network itself. Consequently, it’s evident that the power gain is independent of Zs. However, a common query arises: What happens if Zs is altered?

Imagine altering Zs. Initially, the input impedance (Zin) remains constant. Consequently, any change in Zs would likely result in a decrease in the power delivered to the network (Pin), especially if the initial matching conditions are disrupted.

Now, let’s scrutinize the scenario further. As Pin diminishes, one might assume a corresponding decrease in output power (PL). This assumption aligns with the understanding that the amplifier’s function is to amplify the input power.

However, a remarkable revelation emerges: despite the decrease in Pin, the power gain (G), represented as PL/Pin, remains constant. Why? Because the ratio between PL and Pin persists despite fluctuations in individual magnitudes. In simpler terms, if Pin decreases due to a change in Zs, and subsequently, PL decreases, the ratio PL/Pin remains constant.

This phenomenon underscores a fundamental aspect of power gain: its resilience to variations in source impedance. Despite changes in input conditions, the ratio between output power and input power, indicative of the amplifier’s efficiency, remains steadfast. Thus, while Zs may fluctuate, the integrity of the power gain endures, ensuring consistent performance and reliable amplification.