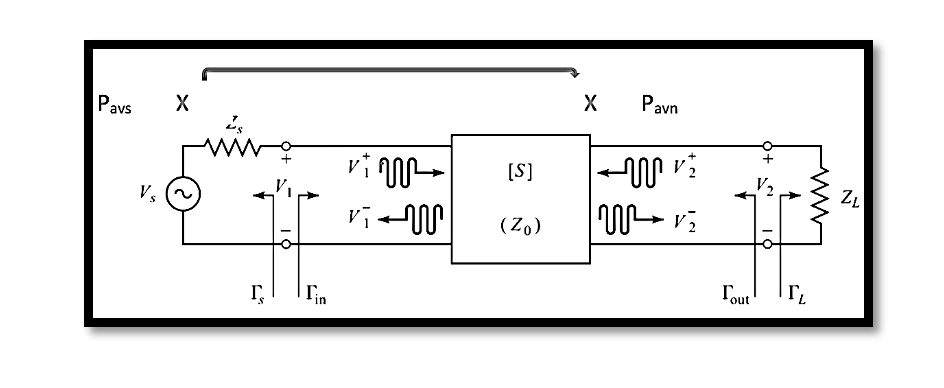
Available Power Gain

Available power gain, denoted as GA​, is a crucial parameter in evaluating the efficiency of power transfer within a network. It’s pivotal to comprehend its equation and significance for optimizing system performance.

Equation and Definition

The formula for available power gain is expressed as the ratio of available power at the output to the available power at the source: GA​=Pavn/​Pavs​​. Here, Pavs​ represents the available power at the source, which essentially denotes the maximum power that can be supplied to the network. This power, often termed Pmax​, signifies the maximum power delivered by the source, such as an amplifier.

Understanding Available Power at Source

Diving deeper into Pavs​, it stands as the maximum power deliverable to the network. In essence, it embodies the power capability of the source, highlighting its vital role in driving the system.

Available Power from the Network

On the other hand, Pavn​ represents the available power from the network. This metric reflects the maximum power that can be transferred to the load (ZL​), signifying the efficiency of power delivery through the network.

Both Pavs​ and Pavn​ serve as pivotal parameters, elucidating the maximum power transfer capability of the system. Understanding these definitions lays a robust foundation for optimizing power transfer efficiency within networks.

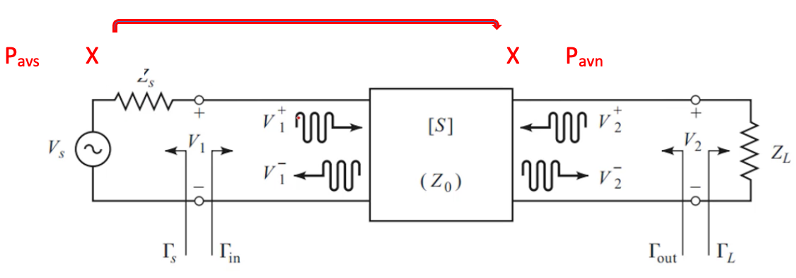
Dependence of Available Power Gain on Network Impedance

The available power gain, as the ratio of power available from the two-port network to the power available from the source, exhibits a notable dependence on the impedance of the source (ZS​) rather than the load (ZL​). This dependency becomes apparent when analyzing the power flow within the two-port network, particularly from Pavs​ to Pavn​.

Understanding Power Flow

Examining the power flow diagram within the two-port network, depicted in the accompanying diagram, elucidates the significance of ZS​ in determining the available power gain. Altering ZS​ inevitably influences the input power delivered to the network, thus affecting the available power at the output.

Role of ZS​

The input power delivered to the network is contingent upon ZS​, emphasizing its pivotal role in determining the available power gain. Any variation in ZS​ leads to a consequential adjustment in the delivered power, thereby impacting the overall gain of the system.

Independence from ZL​

Contrary to ZS​, the available power gain remains independent of ZL​. This assertion might initially appear perplexing, but a closer examination clarifies the distinction. The maximum power available at the output of the network (Pmax​) remains constant irrespective of ZL​. While achieving maximum power transfer necessitates matching Zout​ with ZL​, the value of Pmax​ remains unaltered. Pmax​ signifies the inherent power capability of the network, unaffected by load impedance variations.

In essence, the available power gain’s dependency on ZS​ underscores the significance of source impedance in dictating power transfer efficiency within the network. Conversely, the independence from ZL​ highlights the inherent power capacity of the network, encapsulated by Pmax​. Understanding these distinctions elucidates the nuanced dynamics governing power transfer within two-port networks.

Understanding Power Definitions

Power within electrical systems can be categorized into two distinct definitions, each serving unique roles in analyzing system performance:

1) Delivered Power: Delivered power represents the energy transferred from the source to the load within the electrical circuit. Its magnitude varies based on the impedance of the load, reflecting the dynamic nature of power transfer in the system. The power delivered (Pdelivered​) to the load (ZL​) can be mathematically expressed as:

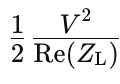
Where V denotes voltage and ZL​ signifies the load impedance. Notably, the delivered power is inherently contingent upon the load impedance, showcasing its dependence on load Characteristics.

2) Available Power: Contrastingly, available power denotes the maximum power capacity that the source can provide to the load. Unlike delivered power, its magnitude remains constant and is independent of the load impedance. Instead, it hinges upon the impedance matching between the source, load, and the electrical circuit.

The available power (PMax​) is akin to the reservoir of power accessible for utilization within the system. Its value remains fixed, representing the pinnacle of power deliverability by the source. Achieving maximum power transfer necessitates impedance matching, ensuring optimal utilization of available power.

Distinguishing Characteristics

• Delivered power fluctuates based on load impedance, reflecting the varying energy transfer within the system.
• Available power remains constant, representing the maximum power potential of the source, independent of load impedance variations.
• Impedance matching is pivotal for maximizing available power utilization, ensuring efficient power transfer within the electrical circuit.

Understanding the distinctions between delivered and available power elucidates the nuanced dynamics governing power transfer efficiency within electrical systems. By optimizing impedance matching, engineers can harness the full potential of available power for enhanced system performance.

Learn more about this topic by taking the complete course ‘Microwave Amplifier and Low Noise Amplifier (LNA) Design Theory and Principles online course – RAHRF526’. Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/. Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.