Understanding Open Loop Bandwidth and Phase Margin in PLL Systems

Introduction

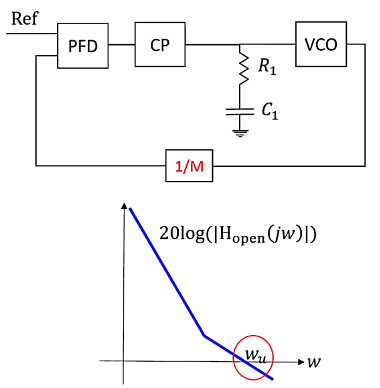
Phase-Locked Loops (PLLs) are essential components in modern electronic systems, widely used in applications ranging from communication systems to signal processing. They are employed to synchronize the frequency of an output oscillator with a reference signal, maintaining a consistent phase relationship. Key to their efficient operation are the concepts of open loop bandwidth and phase margin. These parameters influence system stability, response to phase variations, and the ability to suppress phase noise. This blog explores these concepts in depth, providing detailed calculations and explanations to enhance understanding of PLL system design.

Open Loop Bandwidth

The open loop bandwidth of a PLL system is a critical parameter that affects the system’s performance in several ways:

1. System Stability: Determines the ability of the PLL to remain locked to the reference signal under varying conditions.
2. Response to Phase Variations: Evaluates how the PLL responds to slow and fast phase changes in the reference signal.
3. Phase Noise Suppression: Indicates how effectively the PLL can reduce phase noise within the system.

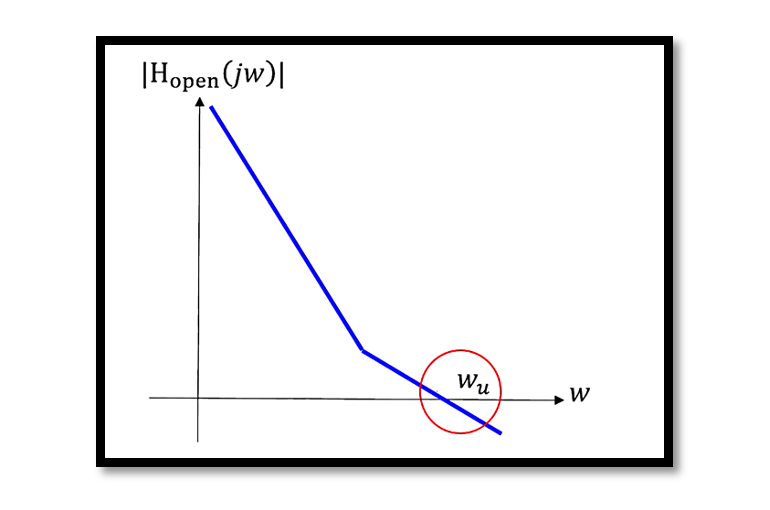
Calculating ωu​

To calculate the open loop bandwidth ωu​, we start with the open loop transfer function Hopen​(jω). The open loop bandwidth is the frequency at which the magnitude of the open loop transfer function is unity:

Where:

• ωn​ is the natural frequency.
• ζ is the damping factor.

Natural Frequency and Damping Factor

The natural frequency ωn and damping factor ζ are fundamental parameters in the design and analysis of PLLs. They are given by:

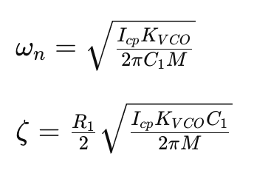
These equations are crucial for determining the open loop bandwidth and understanding the dynamic behavior of the PLL.

Phase Margin

The phase margin (PM) is a measure of the PLL’s stability in the frequency domain. It is calculated based on the phase of the open loop transfer function at the open loop bandwidth frequency ωu​:

Summary of Key Equations

The key equations for analyzing and designing PLL systems are summarized as follows:

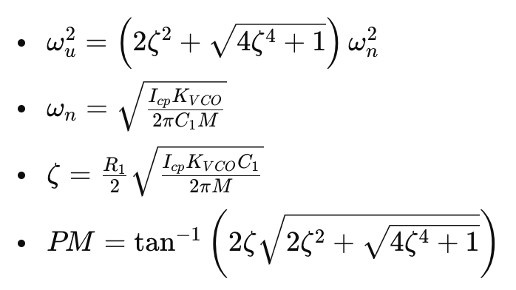
Special Case: ζ≫1

In cases where the damping factor ζ is much greater than 1, the equations simplify significantly, making it easier to analyze the system:

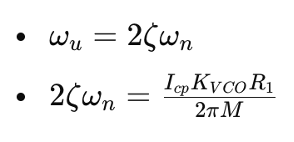
These simplified equations provide valuable insights for designing PLL systems with high damping factors.

Take our entry level course (Below) for free using coupon code RAHRF101BLOG

RF Fundamentals, Basic Concepts and Components – RAHRF101

For limited time take an additional 10% off of all our courses using coupon code RFCERT10

Rahsoft RF Certificate and courses 

Conclusion

Understanding the open loop bandwidth and phase margin is crucial for designing efficient and stable PLL systems. By mastering the calculations and implications of these parameters, engineers can optimize PLL performance, ensuring reliable operation in a wide range of applications. The detailed equations and explanations provided in this blog serve as a comprehensive guide for those looking to deepen their understanding of PLL dynamics.

Learn more about this topic by taking the complete course ‘Phase Lock Loop System Design Theory and Principles RAHRF469’. Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/. Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.