Introduction to Quadrature Modulation and Quadrature Signals

Introduction

In this blog, we are going to discuss quadrature modulation and introduce quadrature signals. We will explore the fundamental meaning of quadrature signals and their use in modulation schemes. Before diving into quadrature modulation, it is essential to understand quadrature signals, their properties, and how they are utilized in modern communication systems.

If you are interested in learning more about these concepts, we offer a comprehensive course titled ‘RF System Design of Receivers, Transmitters & Transceivers – RAHRF409’. This course covers quadrature signals in depth, including their role in image rejection and other key applications. In this blog, we will explain quadrature signals in a simple and intuitive manner, making it easier to grasp their significance and usage in various modulation techniques. For additional insights, you may also read our related blog on Using Quadrature Signals for Down Conversion.

Quadrature Signals: Fundamentals

Quadrature signals, also known as IQ signals, IQ data, or IQ samples, play a crucial role in RF (Radio Frequency) applications. These signals are the foundation of complex RF signal modulation and demodulation, both in hardware and software implementations, as well as in complex signal analysis.

A pair of periodic signals are considered to be in quadrature when they differ in phase by 90 degrees. In this case:

• The first signal, known as the in-phase component (I), serves as the reference signal.
• The second signal, known as the quadrature component (Q), is phase-shifted by 90 degrees relative to the in-phase signal.

This relationship between the in-phase and quadrature signals is widely used in communication systems to efficiently encode and process information.

I and Q Components in Quadrature Signals

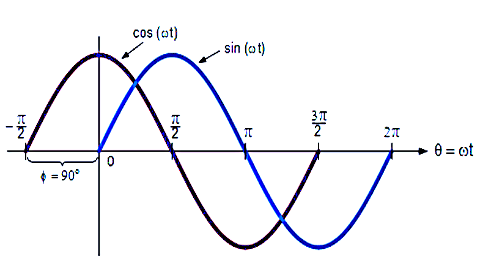
If the phase difference Φ between two sinusoidal signals is 90 degrees (π/2 radians), then these two signals are said to be in quadrature. A typical example of quadrature signals is the sine and cosine waves:

In a modulation system:

• The in-phase signal (I) follows a cosine waveform.
• The quadrature signal (Q) follows a sine waveform.

This orthogonal relationship between I and Q signals allows for the independent modulation of two separate data streams while occupying the same frequency band. Such an approach significantly enhances the spectral efficiency of communication systems.

Adding Quadrature Signals

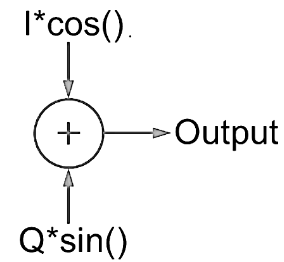
When quadrature signals are combined, their amplitude and phase determine the resultant signal. This is a fundamental principle in quadrature modulation.

Consider the following cases:

• If I = 1 and Q = 0, the resulting waveform is a pure cosine wave with a phase of 0 degrees.
• If I = 0 and Q = 1, the resulting waveform is a pure sine wave, which is 90 degrees phase-shifted.

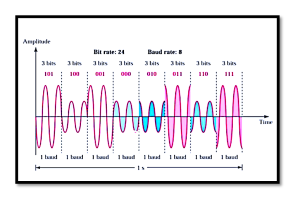
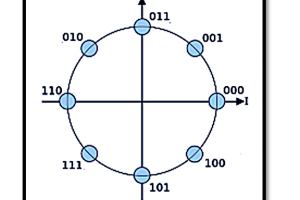
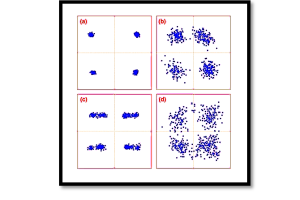
By adjusting the amplitudes of I and Q, we can generate a signal with any desired phase shift. This forms the basis of QAM (Quadrature Amplitude Modulation), PSK (Phase Shift Keying), and other advanced modulation techniques used in modern communication systems.

In mathematical terms, the resultant modulated signal can be expressed as: This formulation demonstrates how the in-phase and quadrature components contribute to the final transmitted signal.

Quadrature Modulation in RF Systems

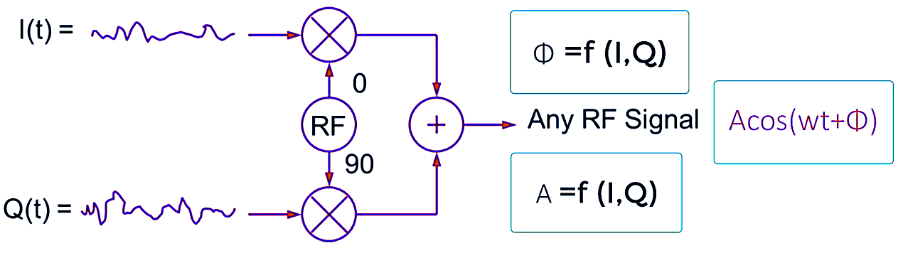
Quadrature modulation is widely used in RF communication because it allows two signals to be transmitted simultaneously over the same carrier frequency. This is achieved by modulating the I and Q signals separately and then summing them to form the final RF signal.

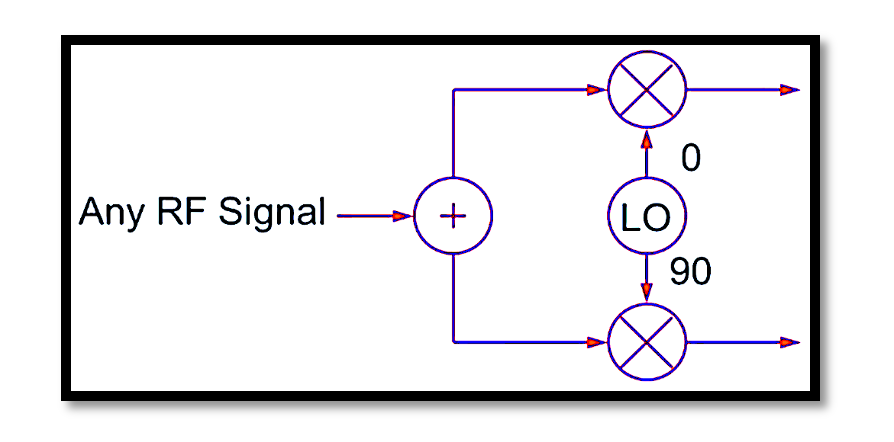
A quadrature modulator consists of:

1. Two multipliers that mix the I and Q signals with carrier waves at 0° and 90° phase shifts, respectively.
2. A summing circuit that combines the modulated signals into a final RF signal.

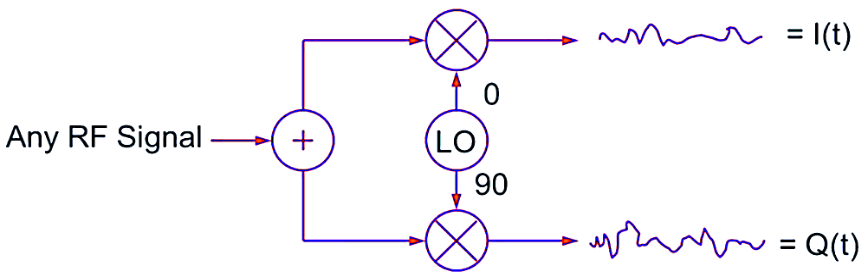
The resultant modulated signal can be expressed as: where A and Φ are functions of the I and Q values. Similarly, a quadrature demodulator can extract the original I and Q signals from the received RF signal using a local oscillator (LO) at the carrier frequency.

Reference: https://www.tek.com/en/blog/quadrature-iq-signals-explained?bpv=2

Applications of Quadrature Modulation

Quadrature modulation techniques are extensively used in:

• Wireless Communication (Wi-Fi, LTE, 5G): Efficiently transmits data using QPSK (Quadrature Phase Shift Keying) and QAM (Quadrature Amplitude Modulation).
• Software-Defined Radios (SDR): Enables flexible modulation and demodulation techniques in digital communication systems.
• Radar Systems: Uses quadrature processing to separate target reflections from noise.

Satellite Communications: Employs QAM and PSK for robust signal transmission over long distances.

Conclusion

Quadrature signals and quadrature modulation form the backbone of modern RF communication systems. By leveraging the orthogonality of sine and cosine waveforms, engineers can efficiently modulate and transmit data with high spectral efficiency. Understanding I and Q signals and their interaction in modulation schemes is essential for designing advanced communication systems. For a more in-depth understanding of quadrature signals and their role in image rejection, modulation, and RF system design, consider enrolling in our course: ‘RF System Design of Receivers, Transmitters & Transceivers – RAHRF409’.

The images and concepts in this blog are referenced from Tektronix’s blog on Quadrature IQ Signals, which provides further detailed insights into quadrature signal applications.

Learn more about this topic by taking the complete course ‘Introduction to Modulation in Communication Systems Online Course – RAHRF152’. Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/. Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.