Understanding Instantaneous and Average Power in AC circuits
Power in circuits
Power by definition is the product of current and voltage in a circuit. Power is an essential aspect to be considered while designing radio frequency and microwave circuits. The main aim while designing a circuit is to have maximum power transfer with minimum loss.
Instantaneous power
The word instantaneously means ‘at once’. Instantaneous power refers to the electric power at any point in time, measured in watts.
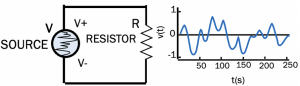
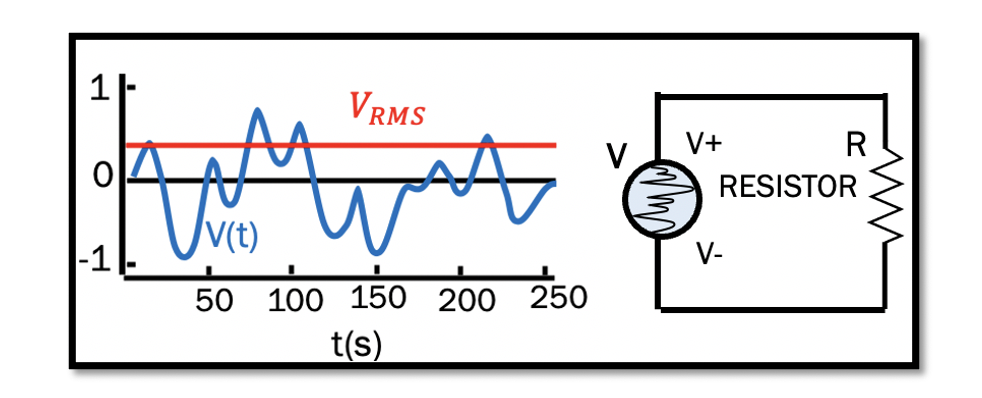
In the above circuit, with a random voltage source and a resistor, the instantaneous power is equal to the product of instantaneous current and instantaneous voltage through it. The power consumed by the Resistor ‘R’ at any instant can be calculated using the equation:

Example: Calculate power when v(t=100) = 2 and R = 50.
-> Calculating instantaneous power using equation (2) we get p(t=100) = 4/50
Average Power
Average power is the integral of instantaneous power over a time ‘T.’ As we are dealing with periodic waveforms like sines and cosines, the time T refers to the time period.
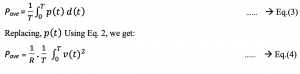
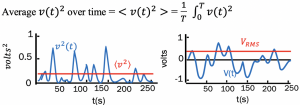
If we take the square root of v(t)2 we can find the vrms (Root Mean Square Voltage). In an AC circuit, the voltage is continually changing. The RMS value gives the average power dissipation in an AC circuit that will be equivalent in the DC circuit.
Example: Calculate RMS value of V(t) = 2cos(ωt) and average power dissipated in 50 ohm resistor.
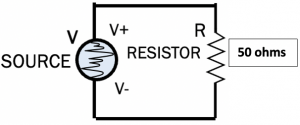
From Eq. 3 & 4, we know:
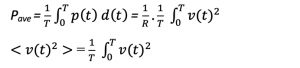
Take a cosine wave representing voltage with a peak value of A, V(t) = Acos(ωt) and substituting the values we get:
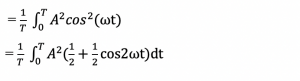
Mathematically, average of cosine wave is 0, so,
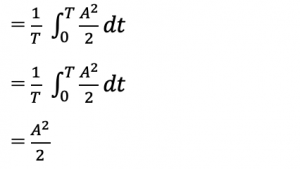
Now calculating the average power Pave , using the above result:
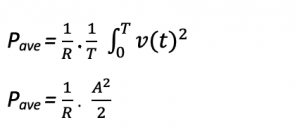
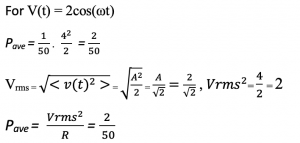
The average power dissipated in the 50 ohm resistor is calculated along with the corresponding RMS value of the voltage and it can also be noted that the average power here is independent of the frequency.

 Learn more about this topic by taking the complete course ‘
Learn more about this topic by taking the complete course ‘