What is Receiver Noise Floor?
Noise Floor:
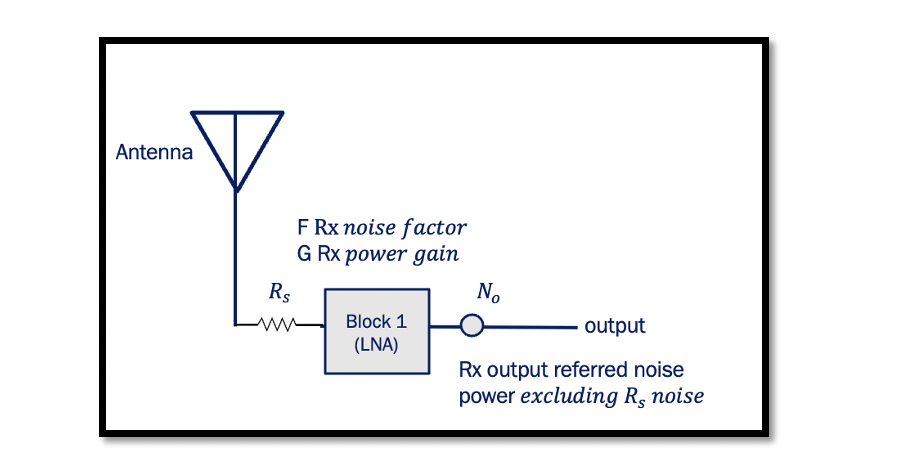
The noise floor is the input-referred total noise power. If we have total noise at the output, we can refer it to the input. Total noise power means that the noise power of the Rs and the noise power of Rx. We have two listed components here that produce noise, one is Rs and the second one is Rx.
Every noise we have in this circuit will be referred to as input, and we call this input-referred noise- noise floor, and we’re going to see how we can calculate it.
We have a noise of Rs, which is already calculated in the previous section, “Receiver chain Noise power,” which is equal to KTB over a bandwidth. As shown in the figure, another factor called ‘No’ refers to the Rx output, referred to as noise power excluding Rs. It means the noise inside Rx will be referred to as the output. Rx is the chain of blocks that can include LNA, Mixer, and other blocks. So ‘No’ doesn’t include the noise of Rs.
F refers to the Noise Factor of the whole chain, which can be calculated using the formula shown below, and G refers to the power gain.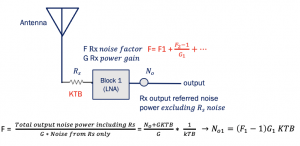
To find the input-referred noise:
At the input, we have the noise of the Rs, which is KTB, and No/G is the input-referred noise of Rx. FKTB is the noise floor (total input-referred noise floor).
This is used to calculate noise in receivers, we just refer all the noise to the input, and we say it is equal to FKTB, where F is the noise factor, K is the Boltzmann constant, T is the temperature in kelvin and B is the bandwidth. So increasing the bandwidth will increase the noise floor, and if we increase the noise floor, the noise factor will increase.
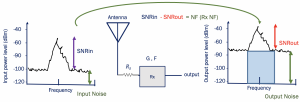
The above figures shows the noise floor with input and output SNR. At the input, we can see that the difference between the signal and the power of the noises SNR at the input is called SNRin as you know, the difference here and is the input noise of the PSD. It’s not the power (for finding the power, we have to integrate it over the bandwidth). When the signal goes through the blocks Rx its SNR degrades because of the noise inside. Assume that you have noise at this point, the noise of Rs, which is going to get amplified along with the signal, so if there is no noise from Rx, the SNR input is going to be equal to SNR output because both signal and noise are being amplified by gain ‘G’ however, this never happens because we have noise in Rx blocks so this noise adds to the previous noise and the SNR decreases.
In the output figure, as you see, the difference between output power and output noise is smaller, and this difference is the difference between input and output SNR is equal to noise figure as known from the definition of noise figure.
Input referred total noise, or noise floor can also be converted to the log domain:

Similarly, the output referred noise can also be calculated in the log domain, which equals to input-referred noise plus the gain:
![]()
Example Question:
Calculate the equivalent input and output noise for the given diagram.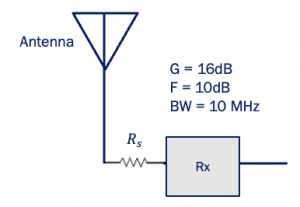
Here the equivalent input refers to the Noise floor:
Noise floor = KTBF
In log domain = -174dBm + 10 log (10 * 106) = -99dBm
Output noise can be calculated by multiplying the gain with the noise floor:
Output noise = KTBF * G
In log domain = -99dBm + 16 =-83dBm

Learn more about this topic by taking the complete course ‘’RF Design Theory and Principles – RAHRF201’’.
Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/
Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.
Tag:Noise Figure, Noise Floor



