Implementing a 90-degree phase shift
How is the 90˚ phase shift implemented?
There are two methods that we will discuss here to implement a 90-degree phase shift inside a receiver. The first method is the RC-CR network and the second method is Quadrature downconversion. In previous blogs, we discussed about Hilbert transform and quadrature downconversion.
1ST METHOD: RC-CR Network
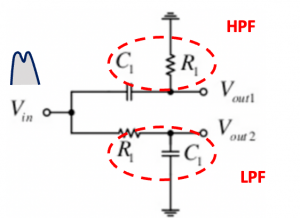
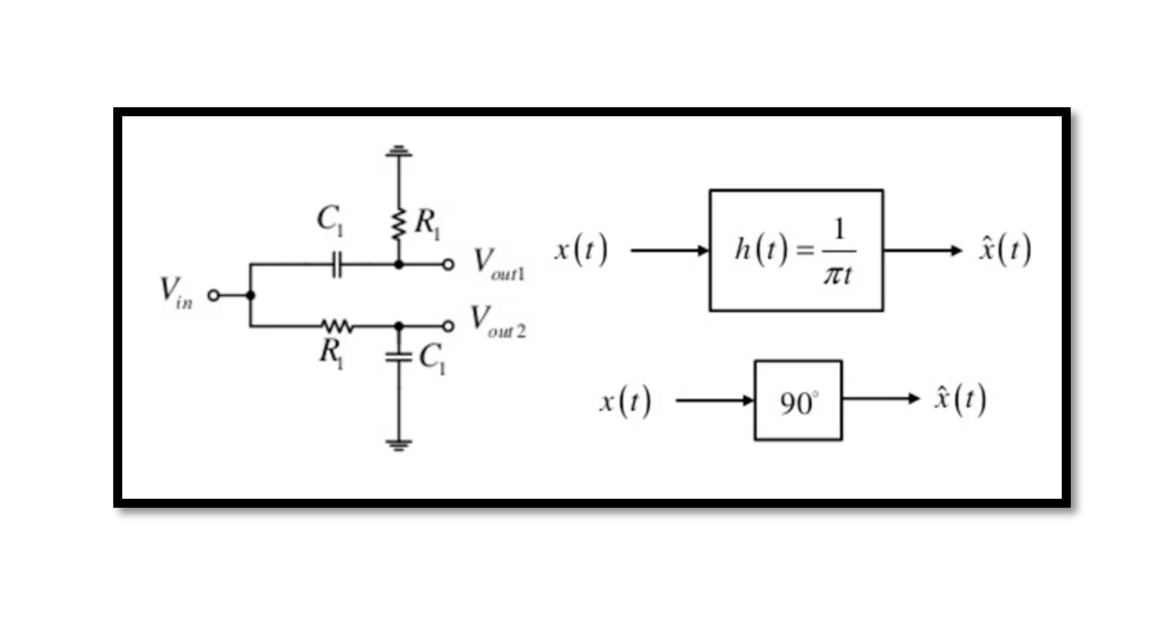
The first method to implement a 90˚ phase shift is to have an RC-CR network. As shown in the figure above, there are two filters, the upper part is the high pass filter (CR) and the lower is the low pass filter (RC). Looking at the amplitude and phase response for this we can see that two signals are produced using one input signal. The amplitude response of these two signals is 1/√2. So they will have the same amplitude but there is only one condition, the channel we have to set 1/R1C1 to be in the center of our channel.
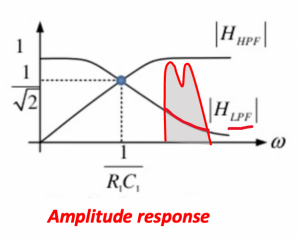
In case the channel is not set to be in this condition what happens then? See the below image, for example, if we have a channel in this region where the low pass filter has a very low response, Vout2 we will have zero response, so it means that system is not working properly.
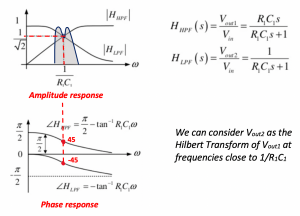
We always trying to operate close to a frequency equal to 1/R1C1. So now we can say that Vout2 is the Hilbert transform of Vout1 at a frequency close to 1/R1C1. Take a look at the phase response here we see these two outputs have exactly a 90-degree phase difference, pointed 45 and minus 45 degrees around 1/R1C1 . We are producing two signals Vout1 and Vout2 which have the same amplitude 1/√2 but 90 degrees phase difference.
2ND METHOD: Quadrature Down conversion
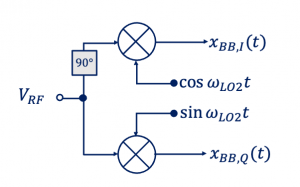
Quadrature down conversion is the second method and preferred method to implement a 90-degree phase shift. We discussed this in our previous blog about Hilbert Transform. Quadrature downconversion translates the spectrum to a non-zero IF as a 90˚ phase shift.
- Creating two versions of a down-converted signal that have a phase difference of 90.
- They are called the “quadrature baseband signals.
- They have identical spectra, and they are separated in phase.
Read about Hilbert transform and quadrature downconversion. This method is preferred over the first method because as mentioned before in the first method that the channels need to be narrow and be close to the value 1/R1C1, plus due to 4 components (RC) involved there would be a mismatch. Read about the mismatch. Hence, using the quadrature down conversion for having a 90-degree phase shift is preferable.
Learn more about this topic by taking the complete course ‘RF System Design of Receivers, Transmitters & Transceivers – RAHRF409’. Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/. Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.
