What is Characteristic Impedance?

What is characteristic impedance in Transmission lines?

In this blog, we are going to talk about the characteristic impedance of a transmission line. Let’s derive the formula for characteristic impedance by finding the relationship between current and voltage from the equations in the previous blog ‘’Transmission line phasor equations’’.

We reached the phasor form equations where we have V(z) and I(z) and later we obtained the equation for V(z) which will be replaced in the below equations as shown:

Now we reached equation (3), so now we can use this equation to define characteristic impedance. We have equation (4) in such form as: 1/Z₀ + voltage, so characteristic impedance can be defined as the ratio of voltage amplitudes and current of a wave propagating along a line. So we basically are just dividing voltage by current and we call this ratio characteristic impedance.

Characteristic impedance is not like L C or R, it’s not physical impedance you can say. For example, say we can get our voltage at some point on the transmission line and divide it by the current at the same point, and we’re going to have a characteristic impedance.

From this formula we have a voltage at a certain point we have a current at the same point at the same location and we just have to divide them the characteristic impedance is going to be the ratio and from here you can also make another expression that shows that the voltage and current phasers on the line are related by the characteristic impedance:

So V_o⁺ / I_o⁺ means both in the positive direction and minus means there in a negative direction if you just if you just divide these phasers you are going to reach your characteristic impedance. There are two definitions; the first one is wavelength on the line and the second one is phase velocity.

Wavelength on the line and Propagation velocity / Phase Velocity

The wavelength of an electromagnetic wave is equal to propagation speed or propagation velocity by frequency. The propagation velocity in the open air is equal to the speed of light. Hence, for electromagnetic waves, the wavelength will be equal to c/ƒ, where c is the speed of light here. If the frequency increases the wavelength decreases.

What is propagation velocity?

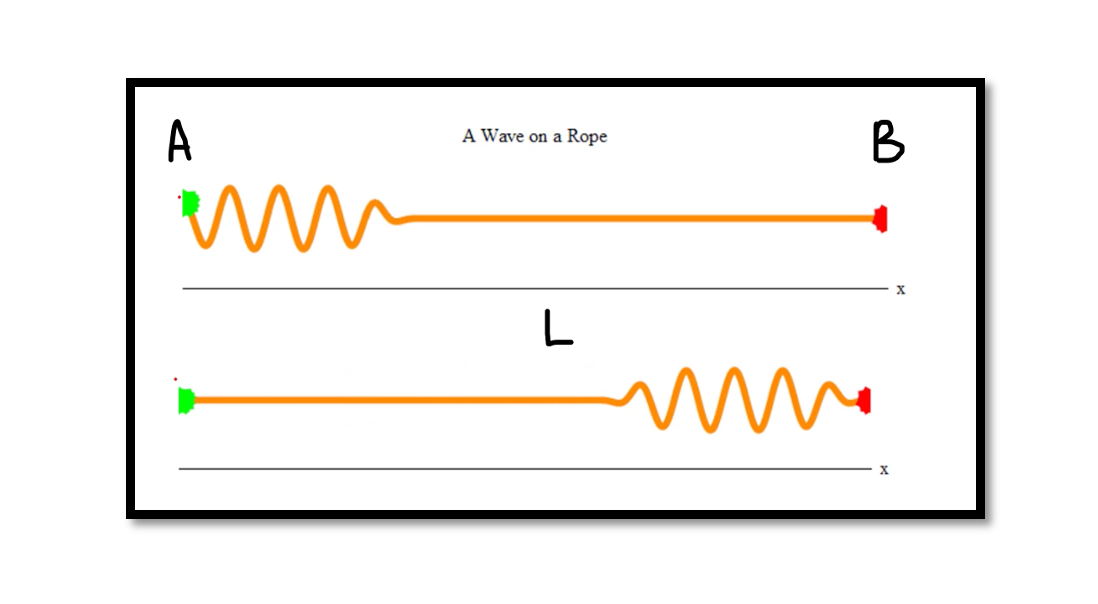
The propagation velocity is very simple for example as shown below we have a rope and using that we produce a wave that travels over a distance, so it has a speed, let’s see the wave propagation on a rope.

The green point A is where the wave is produced and starts moving toward the red point so the distance between points A and B is L. It will take some time for the wave to travel across. So if x is the distance, V is the speed and T is time, then we can say x=V*T. So you can write L is equal to V * T. L is the distance from point A to B and V is a propagation velocity.

The speed of the wave in the open air is equal to the speed of light but the speed will be less if the transmission line has a velocity factor of less than one. Velocity factor (α) is a coefficient, so V_p on the transmission line is equal to α*c where alpha is a velocity factor and is going to be less than one (α <1).

Then instead of replacing it with the speed of light, we’re going to call it V_p the propagation velocity in the transmission line so the wavelength on the line is going to be equal to V_p /ƒ. The propagation velocity or phase velocity is equal to omega (w) by beta (ß). Omega (w) is angular frequency 2πƒ where ƒ is our frequency. From the previous blog, we know that the transmission coefficient gamma (γ) is equal to α+ßj so from here we can find the ß and if we know L, R, C, and G we can find γ. Propagation velocity depends on our components and transmission line, if it is narrow or wide it will have different values for L, R, C, and G which will also affect the propagation velocity. From the equations, we can also find the wavelength which equals 2π/ß.

In the next section, we’re going to talk about lossless lines with some examples to calculate the propagation velocity and characteristic impedance.

Learn more about this topic by taking the complete course ‘RF Microwave and Radio Frequency Transmission Theory Online Course – RAHRF200’. Watch the course videos for more detailed understanding. Also checkout other courses on RF system and IC design on https://rahsoft.com/courses/. Rahsoft also provides a certificate on Radio Frequency. All the courses offer step by step approach.