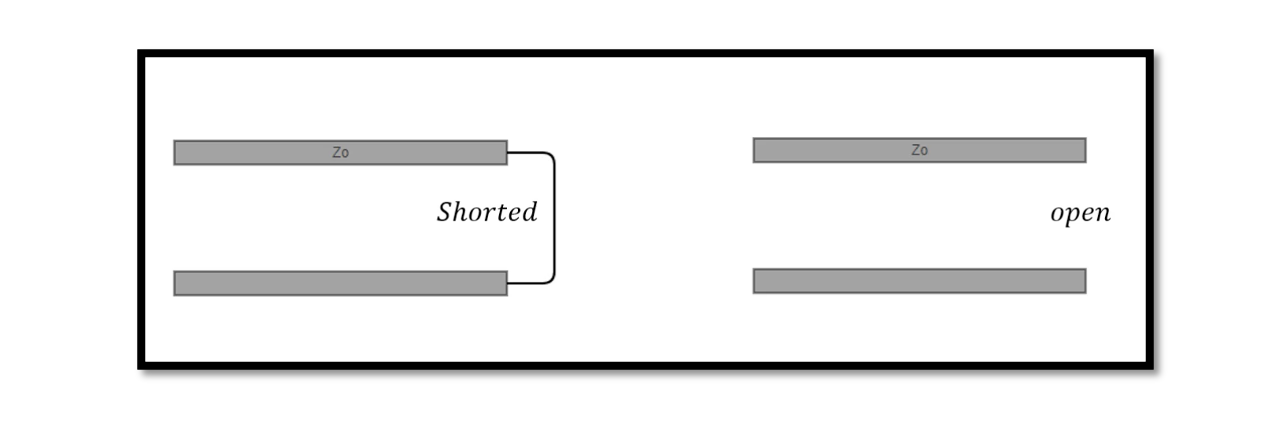
Special Cases of Lossless Transmission Lines
There are two special cases of lossless terminated lines which we will be discussing in this blog. Assume that one of the transmission lines is shorted at one end that means impedance ZL=0 and the other one is open at one end that means impedance ZL=infinity. Explain these two cases using reflection coefficient equations and use them in matching.
Special Case 1: Shorted Transmission Line
Consider two identical transmission lines, each with characteristic impedance Z0, terminated at one end with an unknown impedance ZL. One of the transmission lines is shorted at one end, which means the impedance ZL is zero. The reflection coefficient Γ for the shorted transmission line is given by:
Γ = (ZL – Z0) / (ZL + Z0) = -1
Since the transmission line is shorted, the voltage at the input end of the shorted line is zero, and all of the incident energy is reflected back towards the source. The reflected wave has the same amplitude as the incident wave but is 180 degrees out of phase. The reflection coefficient of -1 indicates that the reflected wave has the same magnitude as the incident wave but opposite sign.
In the case of matching, the shorted transmission line can be used to transform the impedance of the load to the characteristic impedance of the transmission line. If the load impedance is ZL = Z0 / 2, then the reflection coefficient is Γ = (ZL – Z0) / (ZL + Z0) = -1/3. By placing a shorted transmission line between the load and the source, the impedance seen at the source end of the line is Zin = Z0 (1 – Γ) / (1 + Γ) = 2Z0 / 3, which matches the characteristic impedance of the transmission line.
Special Case 2: Open Transmission Line
Consider two identical transmission lines, each with characteristic impedance Z0, terminated at one end with an unknown impedance ZL. One of the transmission lines is open at one end, which means the impedance ZL is infinite. The reflection coefficient Γ for the open transmission line is given by:
Γ = (ZL – Z0) / (ZL + Z0) = 1
Since the transmission line is open, there is no current flowing at the input end of the open line, and all of the incident energy is reflected back towards the source. The reflected wave has the same amplitude as the incident wave but is 180 degrees out of phase. The reflection coefficient of 1 indicates that the reflected wave has the same magnitude as the incident wave but opposite sign.
In the case of matching, the open transmission line can be used to transform the impedance of the load to the characteristic impedance of the transmission line. If the load impedance is ZL = 2Z0, then the reflection coefficient is Γ = (ZL – Z0) / (ZL + Z0) = 1/3. By placing an open transmission line between the load and the source, the impedance seen at the source end of the line is Zin = Z0 (1 + Γ) / (1 – Γ) = Z0 / 3, which matches the characteristic impedance of the transmission line.




